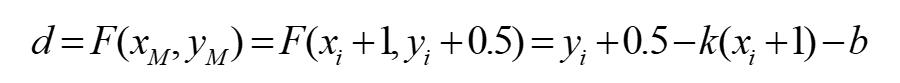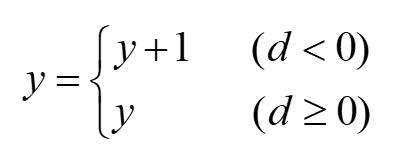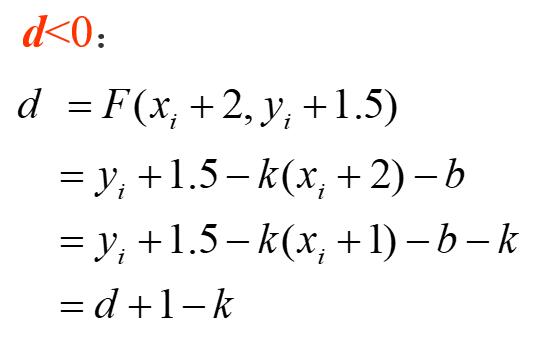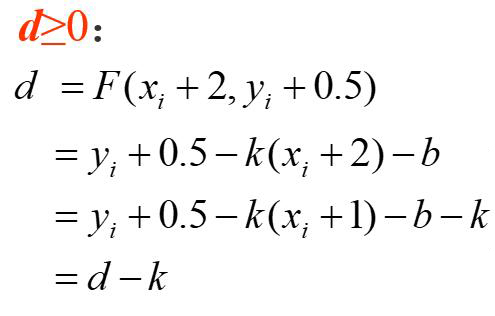最近正在看P5.js这个库，这个库可以说是Processing的JS版。这个库有一套作画功能，不仅仅能在canvas上画，还能把整个浏览器都当成画布。然后对前端数据可视化方向有一些兴趣，再加上开的一门课叫计算机图形学。多者结合，才有了这样一篇文章的整理。

DDA算法

DDA算法原理

DDA算法，是一种通过多个点连成一条近似直线的算法。众所周知，一个图像的显示是由无数个像素点构成的。那么，直线也不例外，也可以看成是无数个点的集合。

DDA算法即选出Δx和Δy中较大者作为最大步长，然后分别与Δx和Δy相乘得出每个方向上的单步步长，将第二个点的坐标算出来后，四舍五入近似成+0或+1。
举个例子，根据上述公式可以看出，假若斜率小于1，每次x单步步长必为+1，此时只考虑y步长，算出y步长后加在上一个点上，然后使用函数进行近似，即可得出点的近似位置

DDA算法实现步骤

  1. 给出两点坐标
  2. 选出Δx和Δy中较大者作为最大步长
  3. 算出x轴和y轴的单步步长
  4. 循环画点

代码实现

效果图

整体看似乎没有什么区别，那么放大看一下

放大看还是能看出比较明显的像素点的，反观line()函数画出的直线则几乎没有锯齿，目前还不清楚line()函数是如何实现的。

HTML

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
<!-- index.html -->
<!DOCTYPE html>
<html lang="">
  <head>
    <meta charset="utf-8">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>DDA算法绘制直线</title>
    <style> body {padding: 0; margin: 0;} </style>
    <script src="../p5/p5.min.js"></script>
    <script src="../p5/addons/p5.dom.min.js"></script>
    <script src="../p5/addons/p5.sound.min.js"></script>
    <script src="./sketch.js"></script>
  </head>
  <body>
  </body>
</html>

JS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
// sketch.js
function setup() {
  /* 
    原来对比直线
    (600,100) 到 (1050,400)
  */
  let o1 = {
    x: 600,
    y: 100
  }
  let o2 = {
    x: 1050,
    y: 400
  }
  
  /* 
    新画直线
    (50,100) 到 (500, 400)
  */
  let beginPoint = {
    x: 50,
    y: 100
  };
  let endPoint = {
    x: 500,
    y: 400
  };


  createCanvas(1200, 600);
  background(0);
  
  stroke(255);
  line(o1.x, o1.y, o2.x, o2.y);
  
  // drawLine(beginPoint, endPoint);
  let lineDDA = new Line(beginPoint, endPoint);
  lineDDA.drawLine();

}

function draw() {

}

class Line {
  constructor(beginPoint, endPoint) {
    // 求Δx和Δy(差)
    this.disX = endPoint.x - beginPoint.x;
    this.disY = endPoint.y - beginPoint.y;
    // 初始点
    this.x = beginPoint.x;
    this.y = beginPoint.y;
  }
  // 最大差值
  getMaxSteps() {
    return (this.disX >= this.disY) ? this.disX : this.disY; 
  }
  // 每次x像素移动长度
  getStepX() {
    return this.disX / this.getMaxSteps();
  }
  // 每次y像素移动长度
  getStepY() {
    return this.disY / this.getMaxSteps();
  }

  drawLine() {
    // 画初始点
    point(this.x, this.y);
    // 循环画点
    for(let i = 1; i <= this.getMaxSteps(); i++) {
      this.x = this.x + this.getStepX();
      this.y = this.y + this.getStepY();
      point(Math.round(this.x), Math.round(this.y));
    }
  }
}

Bresenham算法

0<k<1情况下

Bresenham算法原理

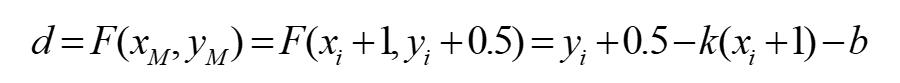
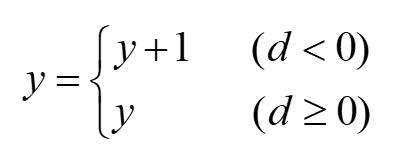
d的递推式：

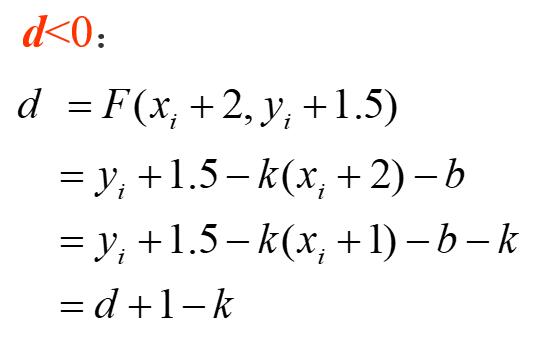
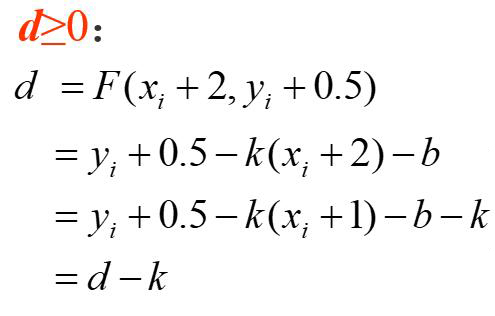
Bresenham算法是对DDA算法的一种改进，避免了取整这一步。算法是通过判别式d的正负来判断直线与坐标轴相交的地方是在中点的上方还是下方（或者左侧还是右侧，根据斜率来判断选择哪一种方式）。倘若在0<k<1的情况下，得出d的值为负，则说明交点在中点上方，此时纵轴步长+1，否则纵轴步长+0。

Bresenham算法实现步骤

0≤k≤1时

  1. 确定直线的两端点
  2. 计算初始值△x、△y、d=0.5-k、x=x0、y=y0
  3. 绘制初始点点(x,y)。判断d的符号,若d<0，则(x,y)更新为(x+1,y+1)，d更新为d+1-k,否则(x,y)更新为(x+1,y)，d更新为d-k
  4. 重复步骤3

代码实现

只有js部分的class部分内容有所改变，其它的都和DDA算法一样，固不再重复列举

效果图

左侧是算法实现，右侧是函数实现

JS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Line {
  constructor(beginPoint, endPoint) {
    // 求Δx和Δy(差)
    this.disX = endPoint.x - beginPoint.x;
    this.disY = endPoint.y - beginPoint.y;
    //斜率
    this.k = this.disY / this.disX;    
    // 初始判别式
    this.d = 0.5 - this.k;
    // 初始点
    this.x = beginPoint.x;
    this.y = beginPoint.y;
  }

  // 最大差值
  getMaxSteps() {
    return (this.disX >= this.disY) ? this.disX : this.disY; 
  }

  drawLine() {
    // 画初始点
    point(this.x, this.y);
    // (k >= 0 ) && (k <= 1) 情况下
    if(this.disX >= this.disY) {
      // 循环画点
      for(let i = 1; i <= this.getMaxSteps(); i++) {
        if(this.d < 0) {
          this.x = this.x + 1;
          this.y = this.y + 1;
          this.d = this.d + 1 - this.k;
        } else {
          this.x = this.x + 1;
          this.y = this.y;
          this.d = this.d - this.k;
        }
        point(this.x, this.y);
      }
    } 
  }
}

总结

这次的实现算是对第一次上图形学课的一点总结，也勉强算是初入图形学的一次入门级的实现吧。